2022年10月20日上午10:00，应1066vip威尼斯邀请，陕西师范大学李瑞教授在线做了题为“偏微分方程数值方法浅谈”的学术报告。报告会由1066vip威尼斯经理李剑教授主持，部分教师及全体研究生参加此次报告。
报告会上，李瑞教授结合丰富经验和研究成果，以泊松方程为例介绍有限差分、有限体积、有限元、间断有限元、弱有限元、虚拟有限元等数值方法以及数值方法发展历史。首先李瑞教授从网格剖分-数值离散格式-刚度矩阵和右端列项组合-数值结果可视化介绍重心对偶的有限体积和有限元方法超逼近，非协调有限体积和C2有限元超逼近，间断有限体积和间断有限元超逼近等结论。其次通过图例展示矩形网格剖分（原始网格剖分、外心对偶剖分（FDM）），三角形网格剖分（原始剖分、外心对偶剖分-直接推广有限差分（FDM）、重心对偶剖分（FVEM）、非协调对偶剖分、间断对偶剖分）的联系和区别。之后介绍在弱有限元基础上发展的杂交高阶有限元方法，其区别在于修改弱梯度部分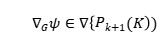
。最后总结了传统网格剖分方法有FDM、FEM、FVEM、DFVEM、WGFEM，任意多边形网格剖分方法有DGFEM、WGFEM、VEM、HHO，并介绍简单便利的程序书写习惯，通过数值算验证了该方法的高效性和低误差性。
李瑞教授生动精彩、深入浅出的讲解引起部分教师的热烈讨论，营造了良好的交流与学习氛围，与会师生受益匪浅。
个人简介：
李瑞，男，陕西师范大学副教授，硕士生导师。2012年6月毕业于河南大学数学与信息科学学院，获得学士学位，2017年12月毕业于西安交通大学数学与统计学院并获得博士学位。主要研究方向是偏微分方程理论与计算、多场耦合问题可计算建模、数值方法程序设 计与实现。在《Journal of Scientific Computing》、 《Advances in Computational Mathematics)》、《Applied Numerical Mathematics》等国内外期刊发表研究论文20余篇。主持国家自然科学基金青年基金1项，陕西省(自然科学基础研究、高校科协青年人才托举)项目2项， 开放基金(中国石化石油物探技术研究院) 2项。获陕西省高等学校 科学技术奖一等奖1项(第二完成人)。
